ノート
完全なサンプルコードをダウンロードするには、ここをクリックしてください
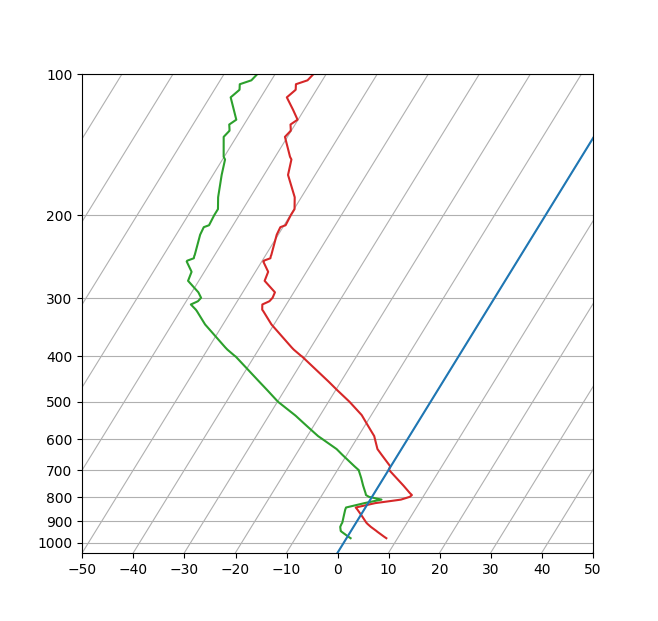
SkewT-logP ダイアグラム: 変換とカスタム プロジェクションの使用#
これは、Matplotlib の変換とカスタム プロジェクション API の集中的な演習として機能します。この例では、いわゆる SkewT-logP ダイアグラムを生成します。これは、気温の垂直プロファイルを表示するための気象学で一般的なプロットです。Matplotlib に関する限り、複雑さは X 軸と Y 軸が直交していないことに起因します。これは、基本的な Axes 変換に傾斜コンポーネントを含めることで処理されます。上部と下部の X 軸のデータ範囲が異なるという事実を処理する際には、さらに複雑になります。これを処理するには、ティック、スパイン、および軸のカスタム クラスが必要になります。
from contextlib import ExitStack
from matplotlib.axes import Axes
import matplotlib.transforms as transforms
import matplotlib.axis as maxis
import matplotlib.spines as mspines
from matplotlib.projections import register_projection
# The sole purpose of this class is to look at the upper, lower, or total
# interval as appropriate and see what parts of the tick to draw, if any.
class SkewXTick(maxis.XTick):
def draw(self, renderer):
# When adding the callbacks with `stack.callback`, we fetch the current
# visibility state of the artist with `get_visible`; the ExitStack will
# restore these states (`set_visible`) at the end of the block (after
# the draw).
with ExitStack() as stack:
for artist in [self.gridline, self.tick1line, self.tick2line,
self.label1, self.label2]:
stack.callback(artist.set_visible, artist.get_visible())
needs_lower = transforms.interval_contains(
self.axes.lower_xlim, self.get_loc())
needs_upper = transforms.interval_contains(
self.axes.upper_xlim, self.get_loc())
self.tick1line.set_visible(
self.tick1line.get_visible() and needs_lower)
self.label1.set_visible(
self.label1.get_visible() and needs_lower)
self.tick2line.set_visible(
self.tick2line.get_visible() and needs_upper)
self.label2.set_visible(
self.label2.get_visible() and needs_upper)
super().draw(renderer)
def get_view_interval(self):
return self.axes.xaxis.get_view_interval()
# This class exists to provide two separate sets of intervals to the tick,
# as well as create instances of the custom tick
class SkewXAxis(maxis.XAxis):
def _get_tick(self, major):
return SkewXTick(self.axes, None, major=major)
def get_view_interval(self):
return self.axes.upper_xlim[0], self.axes.lower_xlim[1]
# This class exists to calculate the separate data range of the
# upper X-axis and draw the spine there. It also provides this range
# to the X-axis artist for ticking and gridlines
class SkewSpine(mspines.Spine):
def _adjust_location(self):
pts = self._path.vertices
if self.spine_type == 'top':
pts[:, 0] = self.axes.upper_xlim
else:
pts[:, 0] = self.axes.lower_xlim
# This class handles registration of the skew-xaxes as a projection as well
# as setting up the appropriate transformations. It also overrides standard
# spines and axes instances as appropriate.
class SkewXAxes(Axes):
# The projection must specify a name. This will be used be the
# user to select the projection, i.e. ``subplot(projection='skewx')``.
name = 'skewx'
def _init_axis(self):
# Taken from Axes and modified to use our modified X-axis
self.xaxis = SkewXAxis(self)
self.spines.top.register_axis(self.xaxis)
self.spines.bottom.register_axis(self.xaxis)
self.yaxis = maxis.YAxis(self)
self.spines.left.register_axis(self.yaxis)
self.spines.right.register_axis(self.yaxis)
def _gen_axes_spines(self):
spines = {'top': SkewSpine.linear_spine(self, 'top'),
'bottom': mspines.Spine.linear_spine(self, 'bottom'),
'left': mspines.Spine.linear_spine(self, 'left'),
'right': mspines.Spine.linear_spine(self, 'right')}
return spines
def _set_lim_and_transforms(self):
"""
This is called once when the plot is created to set up all the
transforms for the data, text and grids.
"""
rot = 30
# Get the standard transform setup from the Axes base class
super()._set_lim_and_transforms()
# Need to put the skew in the middle, after the scale and limits,
# but before the transAxes. This way, the skew is done in Axes
# coordinates thus performing the transform around the proper origin
# We keep the pre-transAxes transform around for other users, like the
# spines for finding bounds
self.transDataToAxes = (
self.transScale
+ self.transLimits
+ transforms.Affine2D().skew_deg(rot, 0)
)
# Create the full transform from Data to Pixels
self.transData = self.transDataToAxes + self.transAxes
# Blended transforms like this need to have the skewing applied using
# both axes, in axes coords like before.
self._xaxis_transform = (
transforms.blended_transform_factory(
self.transScale + self.transLimits,
transforms.IdentityTransform())
+ transforms.Affine2D().skew_deg(rot, 0)
+ self.transAxes
)
@property
def lower_xlim(self):
return self.axes.viewLim.intervalx
@property
def upper_xlim(self):
pts = [[0., 1.], [1., 1.]]
return self.transDataToAxes.inverted().transform(pts)[:, 0]
# Now register the projection with matplotlib so the user can select it.
register_projection(SkewXAxes)
if __name__ == '__main__':
# Now make a simple example using the custom projection.
from io import StringIO
from matplotlib.ticker import (MultipleLocator, NullFormatter,
ScalarFormatter)
import matplotlib.pyplot as plt
import numpy as np
# Some example data.
data_txt = '''
978.0 345 7.8 0.8
971.0 404 7.2 0.2
946.7 610 5.2 -1.8
944.0 634 5.0 -2.0
925.0 798 3.4 -2.6
911.8 914 2.4 -2.7
906.0 966 2.0 -2.7
877.9 1219 0.4 -3.2
850.0 1478 -1.3 -3.7
841.0 1563 -1.9 -3.8
823.0 1736 1.4 -0.7
813.6 1829 4.5 1.2
809.0 1875 6.0 2.2
798.0 1988 7.4 -0.6
791.0 2061 7.6 -1.4
783.9 2134 7.0 -1.7
755.1 2438 4.8 -3.1
727.3 2743 2.5 -4.4
700.5 3048 0.2 -5.8
700.0 3054 0.2 -5.8
698.0 3077 0.0 -6.0
687.0 3204 -0.1 -7.1
648.9 3658 -3.2 -10.9
631.0 3881 -4.7 -12.7
600.7 4267 -6.4 -16.7
592.0 4381 -6.9 -17.9
577.6 4572 -8.1 -19.6
555.3 4877 -10.0 -22.3
536.0 5151 -11.7 -24.7
533.8 5182 -11.9 -25.0
500.0 5680 -15.9 -29.9
472.3 6096 -19.7 -33.4
453.0 6401 -22.4 -36.0
400.0 7310 -30.7 -43.7
399.7 7315 -30.8 -43.8
387.0 7543 -33.1 -46.1
382.7 7620 -33.8 -46.8
342.0 8398 -40.5 -53.5
320.4 8839 -43.7 -56.7
318.0 8890 -44.1 -57.1
310.0 9060 -44.7 -58.7
306.1 9144 -43.9 -57.9
305.0 9169 -43.7 -57.7
300.0 9280 -43.5 -57.5
292.0 9462 -43.7 -58.7
276.0 9838 -47.1 -62.1
264.0 10132 -47.5 -62.5
251.0 10464 -49.7 -64.7
250.0 10490 -49.7 -64.7
247.0 10569 -48.7 -63.7
244.0 10649 -48.9 -63.9
243.3 10668 -48.9 -63.9
220.0 11327 -50.3 -65.3
212.0 11569 -50.5 -65.5
210.0 11631 -49.7 -64.7
200.0 11950 -49.9 -64.9
194.0 12149 -49.9 -64.9
183.0 12529 -51.3 -66.3
164.0 13233 -55.3 -68.3
152.0 13716 -56.5 -69.5
150.0 13800 -57.1 -70.1
136.0 14414 -60.5 -72.5
132.0 14600 -60.1 -72.1
131.4 14630 -60.2 -72.2
128.0 14792 -60.9 -72.9
125.0 14939 -60.1 -72.1
119.0 15240 -62.2 -73.8
112.0 15616 -64.9 -75.9
108.0 15838 -64.1 -75.1
107.8 15850 -64.1 -75.1
105.0 16010 -64.7 -75.7
103.0 16128 -62.9 -73.9
100.0 16310 -62.5 -73.5
'''
# Parse the data
sound_data = StringIO(data_txt)
p, h, T, Td = np.loadtxt(sound_data, unpack=True)
# Create a new figure. The dimensions here give a good aspect ratio
fig = plt.figure(figsize=(6.5875, 6.2125))
ax = fig.add_subplot(projection='skewx')
plt.grid(True)
# Plot the data using normal plotting functions, in this case using
# log scaling in Y, as dictated by the typical meteorological plot
ax.semilogy(T, p, color='C3')
ax.semilogy(Td, p, color='C2')
# An example of a slanted line at constant X
l = ax.axvline(0, color='C0')
# Disables the log-formatting that comes with semilogy
ax.yaxis.set_major_formatter(ScalarFormatter())
ax.yaxis.set_minor_formatter(NullFormatter())
ax.set_yticks(np.linspace(100, 1000, 10))
ax.set_ylim(1050, 100)
ax.xaxis.set_major_locator(MultipleLocator(10))
ax.set_xlim(-50, 50)
plt.show()
参考文献
この例では、次の関数、メソッド、クラス、およびモジュールの使用が示されています。