アシンデモ

変換を使用するasinh軸スケーリングの図

\[a \rightarrow a_0 \sinh^{-1} (a / a_0)\]

ゼロに近い座標値の場合 (つまり、「線形幅」よりもはるかに小さい)\(a_0\))、これにより値は基本的に変更されません。

\[a \rightarrow a + \mathcal{O}(a^3)\]

しかし、より大きな値の場合 (つまり\(|a| \gg a_0\)、これは漸近的に

\[a \rightarrow a_0 \, \mathrm{sgn}(a) \ln |a| + \mathcal{O}(1)\]

スケーリングと同様にsymlog、これにより、正と負の両方の値を含む非常に広いダイナミック レンジをカバーする量をプロットできます。ただし、個別の線形変換と対数変換symlogから構築されているため、勾配に不連続性がある変換が含まれます。スケーリングは、すべての (有限) 値に対して滑らかな変換を使用します。これは、数学的にクリーンであり、プロットの線形領域と対数領域の間の急激な遷移に関連する視覚的なアーティファクトを減らします。asinh

ノート

scale.AsinhScaleは実験的なものであり、API は変更される可能性があります。

AsinhScale、を参照してくださいSymmetricalLogScale。

import numpy as np
import matplotlib.pyplot as plt

# Prepare sample values for variations on y=x graph:
x = np.linspace(-3, 6, 500)

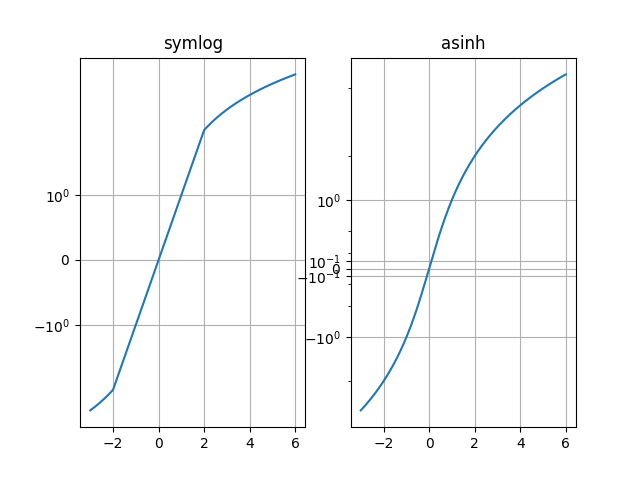
サンプル y=x グラフでの「symlog」と「asinh」の動作を比較します。y=2 付近の「symlog」には不連続な勾配があります。

fig1 = plt.figure()
ax0, ax1 = fig1.subplots(1, 2, sharex=True)

ax0.plot(x, x)
ax0.set_yscale('symlog')
ax0.grid()
ax0.set_title('symlog')

ax1.plot(x, x)
ax1.set_yscale('asinh')
ax1.grid()
ax1.set_title('asinh')

Text(0.5, 1.0, 'asinh')

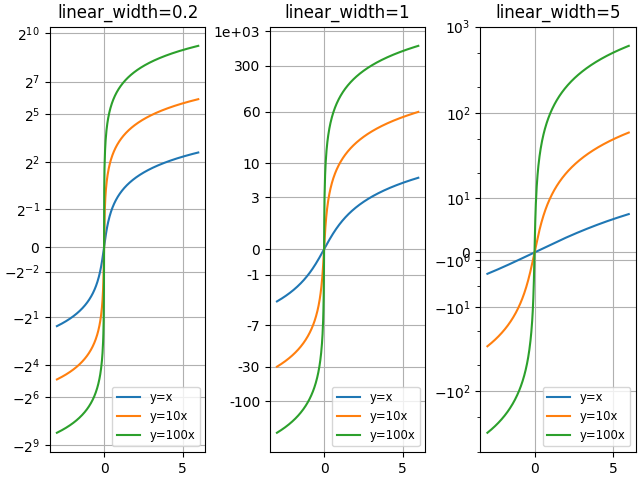
「asinh」グラフを異なるスケール パラメータ「linear_width」で比較します。

fig2 = plt.figure(constrained_layout=True)
axs = fig2.subplots(1, 3, sharex=True)
for ax, (a0, base) in zip(axs, ((0.2, 2), (1.0, 0), (5.0, 10))):
    ax.set_title('linear_width={:.3g}'.format(a0))
    ax.plot(x, x, label='y=x')
    ax.plot(x, 10*x, label='y=10x')
    ax.plot(x, 100*x, label='y=100x')
    ax.set_yscale('asinh', linear_width=a0, base=base)
    ax.grid()
    ax.legend(loc='best', fontsize='small')

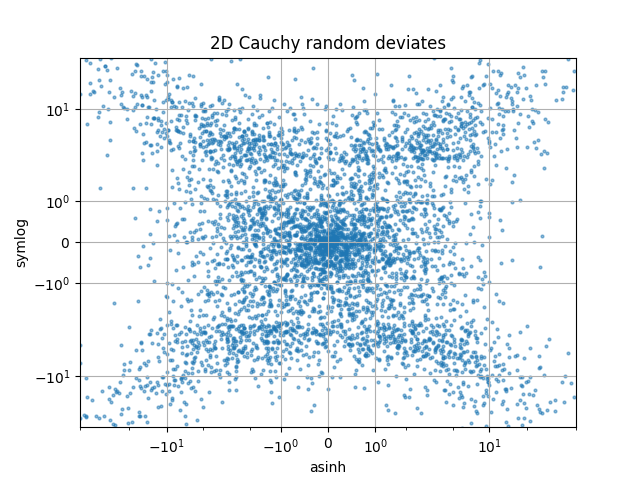
2D コーシー分布の乱数の "symlog" と "asinh" のスケーリングを比較すると、"symlog" の勾配の不連続性により、y=2 付近でより微妙なアーティファクトが見られる場合があります。

fig3 = plt.figure()
ax = fig3.subplots(1, 1)
r = 3 * np.tan(np.random.uniform(-np.pi / 2.02, np.pi / 2.02,
                                 size=(5000,)))
th = np.random.uniform(0, 2*np.pi, size=r.shape)

ax.scatter(r * np.cos(th), r * np.sin(th), s=4, alpha=0.5)
ax.set_xscale('asinh')
ax.set_yscale('symlog')
ax.set_xlabel('asinh')
ax.set_ylabel('symlog')
ax.set_title('2D Cauchy random deviates')
ax.set_xlim(-50, 50)
ax.set_ylim(-50, 50)
ax.grid()

plt.show()

参考文献

• matplotlib.scale.AsinhScale

• matplotlib.ticker.AsinhLocator

• matplotlib.scale.SymmetricalLogScale