ノート
完全なサンプルコードをダウンロードするには、ここをクリックしてください
ヒストグラムを使用して累積分布をプロットする#
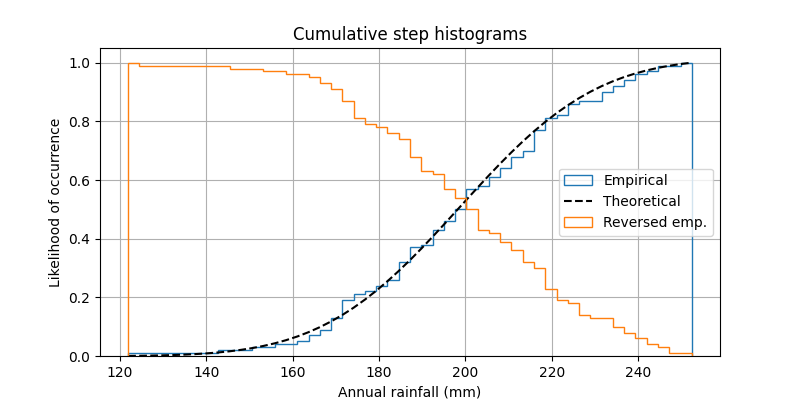
これは、サンプルの経験的累積分布関数 (CDF) を可視化するために、正規化された累積ヒストグラムをステップ関数としてプロットする方法を示しています。また、理論上の CDF も示します。
この関数のその他のオプションがいくつかhist示されています。つまり、ノルムパラメータを使用してヒストグラムを正規化し、いくつかの異なるオプションを累積パラメータに使用します。標準パラメーターはブール値を取ります。の場合True、ビンの高さは、ヒストグラムの合計面積が 1 になるようにスケーリングされます。累積キーワード引数はもう少し微妙です。normedと同様に、True または False を渡すことができますが、分布を逆にするために -1 を渡すこともできます。
正規化された累積ヒストグラムを表示しているため、これらの曲線は事実上、サンプルの累積分布関数 (CDF) です。エンジニアリングでは、経験的CDFは「非超過」曲線と呼ばれることがあります。つまり、指定された x 値の y 値を調べて、その x 値を超えない確率とサンプルからの観測値を取得できます。たとえば、x 軸の 225 の値は y 軸の約 0.85 に対応するため、サンプル内の観測値が 225 を超えない確率は 85% ですcumulative。この例の最後のシリーズは、「超過」曲線を作成します。
異なるビン数とサイズを選択すると、ヒストグラムの形状に大きな影響を与える可能性があります。Astropy のドキュメントには、これらのパラメーターを選択する方法に関する優れたセクションがあります: http://docs.astropy.org/en/stable/visualization/histogram.html
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(19680801)
mu = 200
sigma = 25
n_bins = 50
x = np.random.normal(mu, sigma, size=100)
fig, ax = plt.subplots(figsize=(8, 4))
# plot the cumulative histogram
n, bins, patches = ax.hist(x, n_bins, density=True, histtype='step',
cumulative=True, label='Empirical')
# Add a line showing the expected distribution.
y = ((1 / (np.sqrt(2 * np.pi) * sigma)) *
np.exp(-0.5 * (1 / sigma * (bins - mu))**2))
y = y.cumsum()
y /= y[-1]
ax.plot(bins, y, 'k--', linewidth=1.5, label='Theoretical')
# Overlay a reversed cumulative histogram.
ax.hist(x, bins=bins, density=True, histtype='step', cumulative=-1,
label='Reversed emp.')
# tidy up the figure
ax.grid(True)
ax.legend(loc='right')
ax.set_title('Cumulative step histograms')
ax.set_xlabel('Annual rainfall (mm)')
ax.set_ylabel('Likelihood of occurrence')
plt.show()