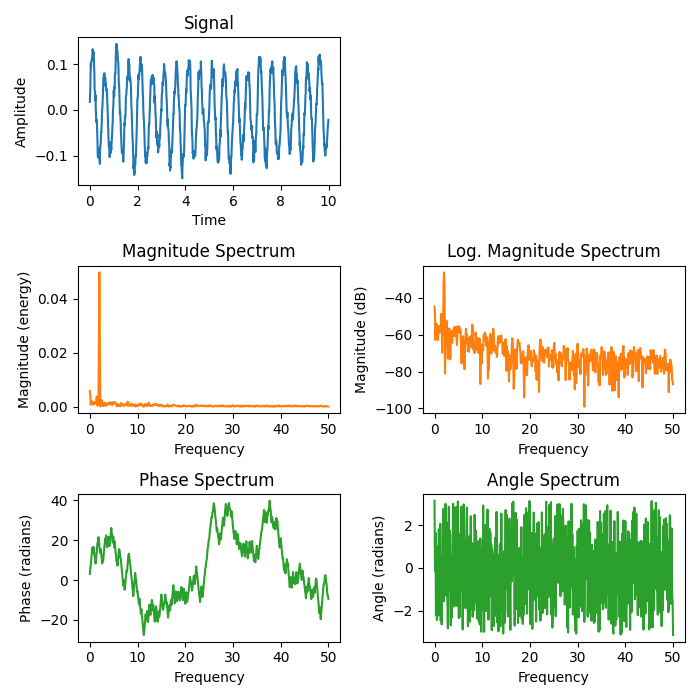
スペクトル表現

プロットは、加法性ノイズを含む正弦波信号のさまざまなスペクトル表現を示しています。離散時間信号の (周波数) スペクトルは、高速フーリエ変換 (FFT) を利用して計算されます。

import matplotlib.pyplot as plt
import numpy as np


np.random.seed(0)

dt = 0.01  # sampling interval
Fs = 1 / dt  # sampling frequency
t = np.arange(0, 10, dt)

# generate noise:
nse = np.random.randn(len(t))
r = np.exp(-t / 0.05)
cnse = np.convolve(nse, r) * dt
cnse = cnse[:len(t)]

s = 0.1 * np.sin(4 * np.pi * t) + cnse  # the signal

fig, axs = plt.subplots(nrows=3, ncols=2, figsize=(7, 7))

# plot time signal:
axs[0, 0].set_title("Signal")
axs[0, 0].plot(t, s, color='C0')
axs[0, 0].set_xlabel("Time")
axs[0, 0].set_ylabel("Amplitude")

# plot different spectrum types:
axs[1, 0].set_title("Magnitude Spectrum")
axs[1, 0].magnitude_spectrum(s, Fs=Fs, color='C1')

axs[1, 1].set_title("Log. Magnitude Spectrum")
axs[1, 1].magnitude_spectrum(s, Fs=Fs, scale='dB', color='C1')

axs[2, 0].set_title("Phase Spectrum ")
axs[2, 0].phase_spectrum(s, Fs=Fs, color='C2')

axs[2, 1].set_title("Angle Spectrum")
axs[2, 1].angle_spectrum(s, Fs=Fs, color='C2')

axs[0, 1].remove()  # don't display empty ax

fig.tight_layout()
plt.show()