3D プロット投影タイプ

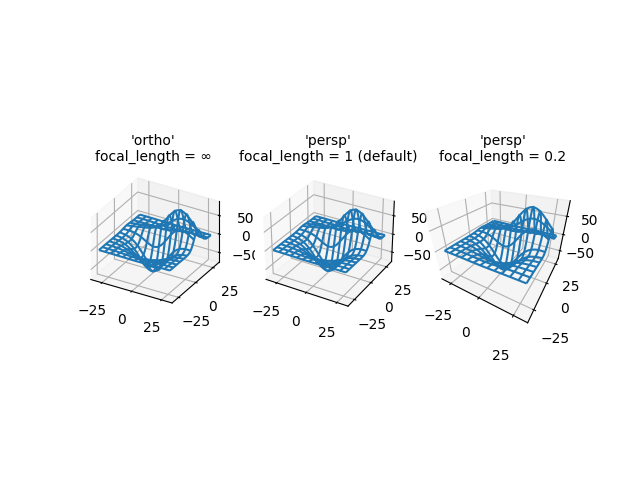
3D プロットのさまざまなカメラ投影と、透視投影の焦点距離の変更の効果を示します。Matplotlib は、焦点距離の変更による「ズーム」効果を補正することに注意してください。

デフォルトの焦点距離 1 は、90 度の視野 (FOV) に対応します。焦点距離が 1 から無限大の間で増加すると、イメージが「平坦」になり、焦点距離が 1 から 0 の間で減少すると、遠近感が誇張され、イメージにより明確な奥行きが与えられます。限定的なケースでは、無限の焦点距離は、ズーム効果の補正後の正投影に対応します。

次の式を使用して、FOV から焦点距離を計算できます。

\[1 / \tan (\mathrm{FOV} / 2)\]

またはその逆:

\[\mathrm{FOV} = 2 \arctan (1 / \mathrm{focal length})\]

from mpl_toolkits.mplot3d import axes3d
import matplotlib.pyplot as plt


fig, axs = plt.subplots(1, 3, subplot_kw={'projection': '3d'})

# Get the test data
X, Y, Z = axes3d.get_test_data(0.05)

# Plot the data
for ax in axs:
    ax.plot_wireframe(X, Y, Z, rstride=10, cstride=10)

# Set the orthographic projection.
axs[0].set_proj_type('ortho')  # FOV = 0 deg
axs[0].set_title("'ortho'\nfocal_length = ∞", fontsize=10)

# Set the perspective projections
axs[1].set_proj_type('persp')  # FOV = 90 deg
axs[1].set_title("'persp'\nfocal_length = 1 (default)", fontsize=10)

axs[2].set_proj_type('persp', focal_length=0.2)  # FOV = 157.4 deg
axs[2].set_title("'persp'\nfocal_length = 0.2", fontsize=10)

plt.show()