ネストされた円グラフ#

次の例は、Matplotlib でネストされた円グラフを作成する 2 つの方法を示しています。このようなグラフは、ドーナツグラフと呼ばれることがよくあります。

import matplotlib.pyplot as plt
import numpy as np

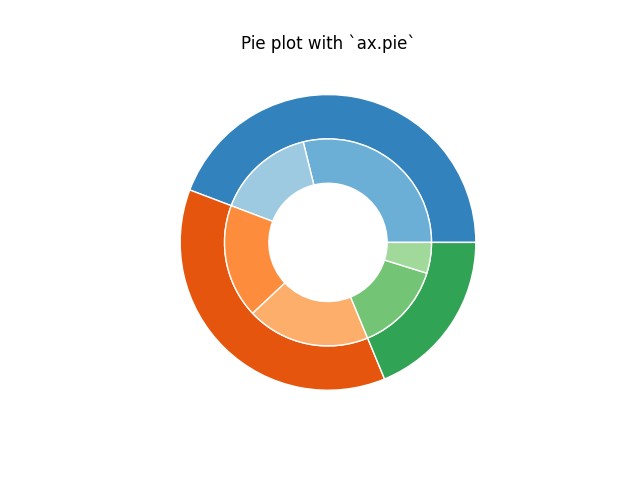
円グラフを作成する最も簡単な方法は、 pieメソッドを使用することです。

この場合、円グラフはグループ内のカウントに対応する値を取ります。最初に、3 つのグループに対応するいくつかの偽のデータを生成します。内側の円では、各数値を独自のグループに属するものとして扱います。外側の円では、元の 3 つのグループのメンバーとしてそれらをプロットします。

ドーナツ形状の効果は、 wedgeprops引数widthを介してパイのウェッジに a を設定することによって実現されます。

fig, ax = plt.subplots()

size = 0.3
vals = np.array([[60., 32.], [37., 40.], [29., 10.]])

cmap = plt.colormaps["tab20c"]
outer_colors = cmap(np.arange(3)*4)
inner_colors = cmap([1, 2, 5, 6, 9, 10])

ax.pie(vals.sum(axis=1), radius=1, colors=outer_colors,
       wedgeprops=dict(width=size, edgecolor='w'))

ax.pie(vals.flatten(), radius=1-size, colors=inner_colors,
       wedgeprops=dict(width=size, edgecolor='w'))

ax.set(aspect="equal", title='Pie plot with `ax.pie`')
plt.show()

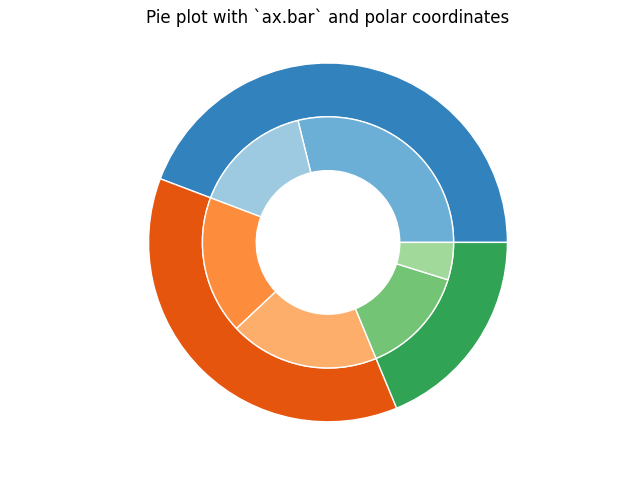
ただし、極座標系の軸にバープロットを使用することで、同じ出力を実現できます。これにより、プロットの正確な設計がより柔軟になります。

この場合、棒グラフの x 値を円のラジアンにマッピングする必要があります。値の累積合計がバーのエッジとして使用されます。

fig, ax = plt.subplots(subplot_kw=dict(projection="polar"))

size = 0.3
vals = np.array([[60., 32.], [37., 40.], [29., 10.]])
# Normalize vals to 2 pi
valsnorm = vals/np.sum(vals)*2*np.pi
# Obtain the ordinates of the bar edges
valsleft = np.cumsum(np.append(0, valsnorm.flatten()[:-1])).reshape(vals.shape)

cmap = plt.colormaps["tab20c"]
outer_colors = cmap(np.arange(3)*4)
inner_colors = cmap([1, 2, 5, 6, 9, 10])

ax.bar(x=valsleft[:, 0],
       width=valsnorm.sum(axis=1), bottom=1-size, height=size,
       color=outer_colors, edgecolor='w', linewidth=1, align="edge")

ax.bar(x=valsleft.flatten(),
       width=valsnorm.flatten(), bottom=1-2*size, height=size,
       color=inner_colors, edgecolor='w', linewidth=1, align="edge")

ax.set(title="Pie plot with `ax.bar` and polar coordinates")
ax.set_axis_off()
plt.show()

参考文献

この例では、次の関数、メソッド、クラス、およびモジュールの使用が示されています。

Sphinx-Gallery によって生成されたギャラリー