カラーマップの正規化

既定でカラーマップを使用するオブジェクトは、カラーマップの色をデータ値vminからvmaxに線形にマッピングします。例えば：

pcm = ax.pcolormesh(x, y, Z, vmin=-1., vmax=1., cmap='RdBu_r')

Zのデータを-1 から +1 まで直線的にマッピングするため、Z=0はカラーマップRdBu_rの中心に色を与えます(この場合は白)。

Matplotlib はこのマッピングを 2 つのステップで行います。入力データから [0, 1] への正規化が最初に行われ、次にカラーマップのインデックスにマッピングされます。matplotlib.colors()正規化は、モジュールで定義されたクラス です。デフォルトの線形正規化はmatplotlib.colors.Normalize()です。

データを色にマッピングするアーティストは、引数vminとvmaxを渡してインスタンスを構築しmatplotlib.colors.Normalize()、それを呼び出します。

In [1]: import matplotlib as mpl

In [2]: norm = mpl.colors.Normalize(vmin=-1, vmax=1)

In [3]: norm(0)
Out[3]: 0.5

ただし、非線形の方法でデータをカラーマップにマッピングすると便利な場合があります。

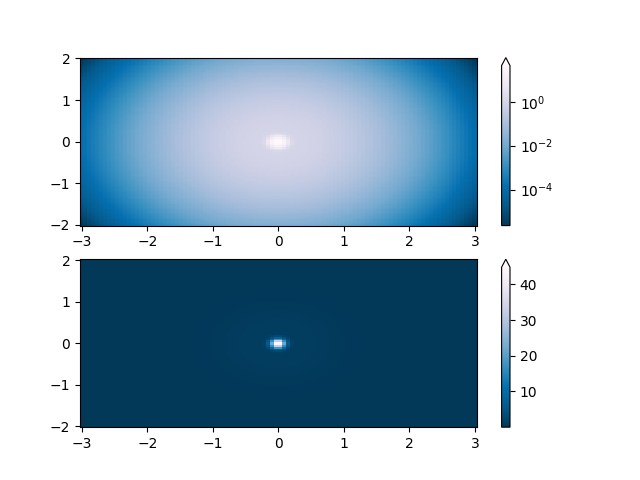
対数

最も一般的な変換の 1 つは、対数 (底 10) をとってデータをプロットすることです。この変換は、異なる縮尺での変更を表示するのに役立ちます。を使用colors.LogNormすると、次の方法でデータが正規化されます \(log_{10}\). 以下の例では、2 つの隆起があり、一方は他方よりもはるかに小さいです。を使用colors.LogNormすると、各バンプの形状と位置が明確にわかります。

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.colors as colors
import matplotlib.cbook as cbook
from matplotlib import cm

N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]

# A low hump with a spike coming out of the top right.  Needs to have
# z/colour axis on a log scale so we see both hump and spike.  linear
# scale only shows the spike.
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X * 10)**2 - (Y * 10)**2)
Z = Z1 + 50 * Z2

fig, ax = plt.subplots(2, 1)

pcm = ax[0].pcolor(X, Y, Z,
                   norm=colors.LogNorm(vmin=Z.min(), vmax=Z.max()),
                   cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')

pcm = ax[1].pcolor(X, Y, Z, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
plt.show()

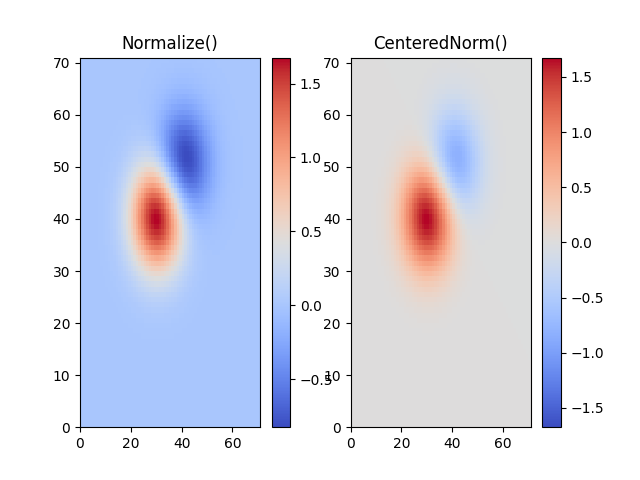
中央揃え

多くの場合、データは中心に対して対称です。たとえば、中心 0 の周りに正と負の異常があります。この場合、中心を 0.5 にマッピングし、中心からの偏差が最大のデータポイントをマッピングします。値が中心よりも大きい場合は 1.0、それ以外の場合は 0.0 になります。規範colors.CenteredNormは、そのようなマッピングを自動的に作成します。不飽和色の中心で交わるさまざまな色のエッジを使用する発散カラーマップと組み合わせるのに適しています。

対称の中心が 0 以外の場合は、 vcenter引数で設定できます。中心の両側の対数スケーリングについては、以下を参照してください colors.SymLogNorm。中心の上下に異なるマッピングを適用するには、以下を使用しcolors.TwoSlopeNormます。

delta = 0.1
x = np.arange(-3.0, 4.001, delta)
y = np.arange(-4.0, 3.001, delta)
X, Y = np.meshgrid(x, y)
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (0.9*Z1 - 0.5*Z2) * 2

# select a divergent colormap
cmap = cm.coolwarm

fig, (ax1, ax2) = plt.subplots(ncols=2)
pc = ax1.pcolormesh(Z, cmap=cmap)
fig.colorbar(pc, ax=ax1)
ax1.set_title('Normalize()')

pc = ax2.pcolormesh(Z, norm=colors.CenteredNorm(), cmap=cmap)
fig.colorbar(pc, ax=ax2)
ax2.set_title('CenteredNorm()')

plt.show()

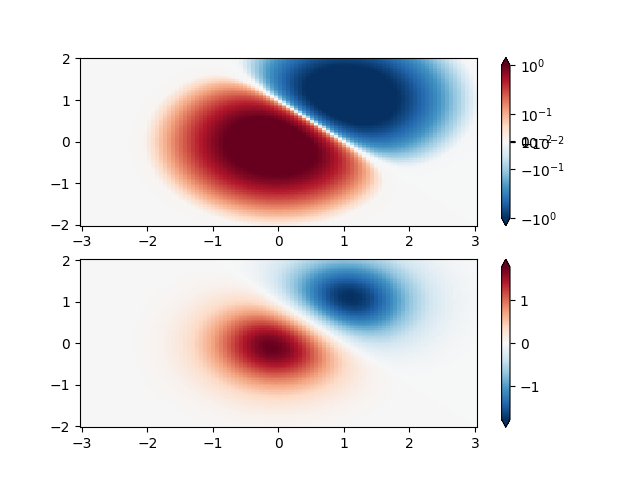
対称対数

同様に、正と負のデータが存在する場合もありますが、両方に対数スケーリングを適用する必要があります。この場合、負の数値も対数的にスケーリングされ、より小さい数値にマップされます。たとえば、 の場合vmin=-vmax、負の数は 0 から 0.5 に、正の数は 0.5 から 1 にマッピングされます。

ゼロに近い値の対数は無限大になる傾向があるため、ゼロ付近の小さな範囲を線形にマッピングする必要があります。パラメータ linthreshを使用すると、ユーザーはこの範囲のサイズを指定できます (- linthresh、linthresh )。カラーマップ内のこの範囲のサイズはlinscaleによって設定されます。linscale == 1.0 (デフォルト) の場合、線形範囲の正と負の半分に使用されるスペースは、対数範囲の 1 ディケードに等しくなります。

N = 100
X, Y = np.mgrid[-3:3:complex(0, N), -2:2:complex(0, N)]
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = (Z1 - Z2) * 2

fig, ax = plt.subplots(2, 1)

pcm = ax[0].pcolormesh(X, Y, Z,
                       norm=colors.SymLogNorm(linthresh=0.03, linscale=0.03,
                                              vmin=-1.0, vmax=1.0, base=10),
                       cmap='RdBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='both')

pcm = ax[1].pcolormesh(X, Y, Z, cmap='RdBu_r', vmin=-np.max(Z), shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='both')
plt.show()

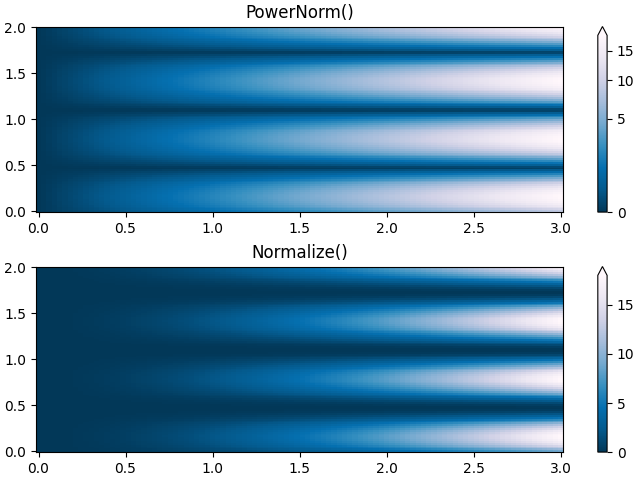
べき法則

色をベキ乗関係に再マッピングすると便利な場合があります (つまり、\(y=x^{\gamma}\)、 どこ\(\gamma\)力です）。これには、 を使用しcolors.PowerNormます。引数としてガンマを取ります(ガンマ== 1.0 はデフォルトの線形正規化を生成します):

ノート

このタイプの変換を使用してデータをプロットするのには、おそらく十分な理由があるはずです。テクニカル ビューアーは、線形軸と対数軸、およびデータ変換に慣れています。べき乗則はあまり一般的ではないため、視聴者はそれらが使用されていることを明示的に認識する必要があります。

N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2

fig, ax = plt.subplots(2, 1, constrained_layout=True)

pcm = ax[0].pcolormesh(X, Y, Z1, norm=colors.PowerNorm(gamma=0.5),
                       cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[0], extend='max')
ax[0].set_title('PowerNorm()')

pcm = ax[1].pcolormesh(X, Y, Z1, cmap='PuBu_r', shading='auto')
fig.colorbar(pcm, ax=ax[1], extend='max')
ax[1].set_title('Normalize()')
plt.show()

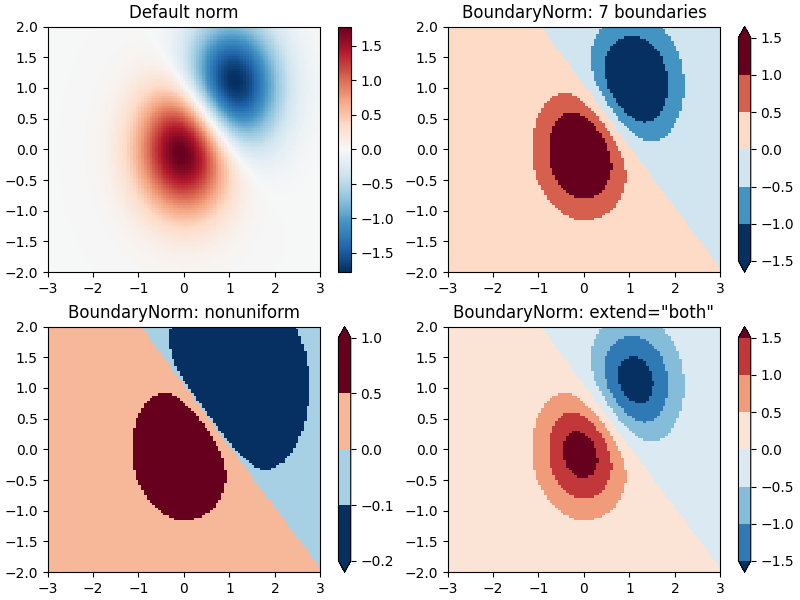
離散境界

Matplotlib に付属する別の正規化はcolors.BoundaryNorm. vminとvmaxに加えて、これはデータがマップされる境界を引数として取ります。色は、これらの「境界」の間で線形に分配されます。また、extend引数を使用して、色が分布する範囲に上限および/または下限の範囲外の値を追加することもできます。例えば：

In [4]: import matplotlib.colors as colors

In [5]: bounds = np.array([-0.25, -0.125, 0, 0.5, 1])

In [6]: norm = colors.BoundaryNorm(boundaries=bounds, ncolors=4)

In [7]: print(norm([-0.2, -0.15, -0.02, 0.3, 0.8, 0.99]))
[0 0 1 2 3 3]

注: 他のノルムとは異なり、このノルムは 0 からncolors -1 までの値を返します。

N = 100
X, Y = np.meshgrid(np.linspace(-3, 3, N), np.linspace(-2, 2, N))
Z1 = np.exp(-X**2 - Y**2)
Z2 = np.exp(-(X - 1)**2 - (Y - 1)**2)
Z = ((Z1 - Z2) * 2)[:-1, :-1]

fig, ax = plt.subplots(2, 2, figsize=(8, 6), constrained_layout=True)
ax = ax.flatten()

# Default norm:
pcm = ax[0].pcolormesh(X, Y, Z, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[0], orientation='vertical')
ax[0].set_title('Default norm')

# Even bounds give a contour-like effect:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[1].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[1], extend='both', orientation='vertical')
ax[1].set_title('BoundaryNorm: 7 boundaries')

# Bounds may be unevenly spaced:
bounds = np.array([-0.2, -0.1, 0, 0.5, 1])
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256)
pcm = ax[2].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
fig.colorbar(pcm, ax=ax[2], extend='both', orientation='vertical')
ax[2].set_title('BoundaryNorm: nonuniform')

# With out-of-bounds colors:
bounds = np.linspace(-1.5, 1.5, 7)
norm = colors.BoundaryNorm(boundaries=bounds, ncolors=256, extend='both')
pcm = ax[3].pcolormesh(X, Y, Z, norm=norm, cmap='RdBu_r')
# The colorbar inherits the "extend" argument from BoundaryNorm.
fig.colorbar(pcm, ax=ax[3], orientation='vertical')
ax[3].set_title('BoundaryNorm: extend="both"')
plt.show()

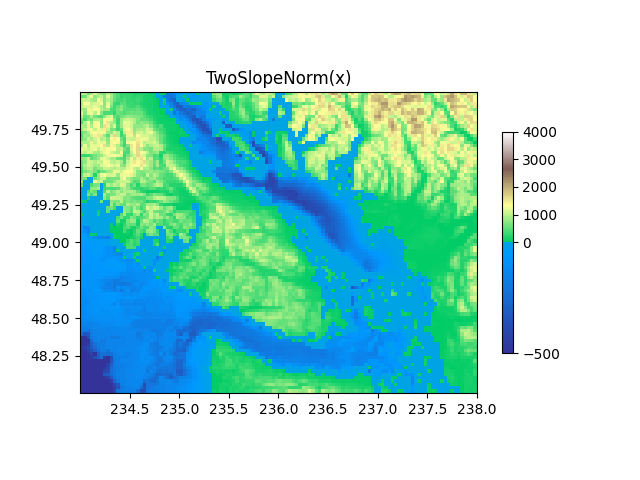
TwoSlopeNorm: 中心の両側で異なるマッピング

概念的な中心点の両側に異なるカラーマップが必要な場合があり、これら 2 つのカラーマップに異なる線形スケールを持たせたい場合があります。例として、陸と海の中心がゼロである地形図がありますが、陸は通常、水域の深度範囲よりも標高範囲が大きく、異なるカラーマップで表されることがよくあります。

dem = cbook.get_sample_data('topobathy.npz', np_load=True)
topo = dem['topo']
longitude = dem['longitude']
latitude = dem['latitude']

fig, ax = plt.subplots()
# make a colormap that has land and ocean clearly delineated and of the
# same length (256 + 256)
colors_undersea = plt.cm.terrain(np.linspace(0, 0.17, 256))
colors_land = plt.cm.terrain(np.linspace(0.25, 1, 256))
all_colors = np.vstack((colors_undersea, colors_land))
terrain_map = colors.LinearSegmentedColormap.from_list(
    'terrain_map', all_colors)

# make the norm:  Note the center is offset so that the land has more
# dynamic range:
divnorm = colors.TwoSlopeNorm(vmin=-500., vcenter=0, vmax=4000)

pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=divnorm,
                    cmap=terrain_map, shading='auto')
# Simple geographic plot, set aspect ratio because distance between lines of
# longitude depends on latitude.
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('TwoSlopeNorm(x)')
cb = fig.colorbar(pcm, shrink=0.6)
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])
plt.show()

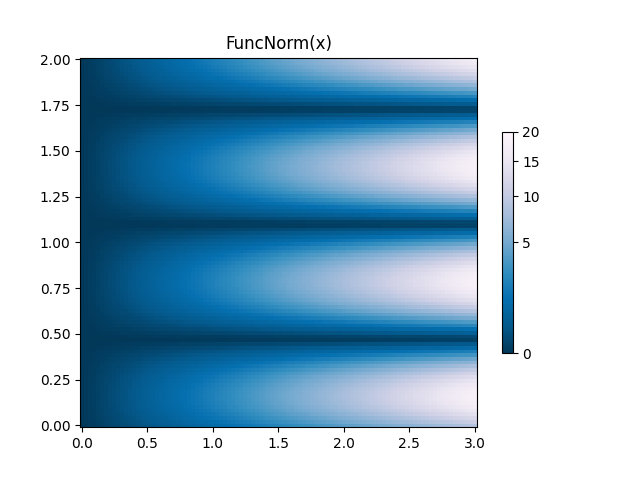
FuncNorm: 任意関数の正規化

上記の基準では希望する正規化が得られない場合は、 を使用 FuncNormして独自の基準を定義できます。この例は、PowerNormべき乗が 0.5 の場合と同じであることに注意してください。

def _forward(x):
    return np.sqrt(x)


def _inverse(x):
    return x**2

N = 100
X, Y = np.mgrid[0:3:complex(0, N), 0:2:complex(0, N)]
Z1 = (1 + np.sin(Y * 10.)) * X**2
fig, ax = plt.subplots()

norm = colors.FuncNorm((_forward, _inverse), vmin=0, vmax=20)
pcm = ax.pcolormesh(X, Y, Z1, norm=norm, cmap='PuBu_r', shading='auto')
ax.set_title('FuncNorm(x)')
fig.colorbar(pcm, shrink=0.6)
plt.show()

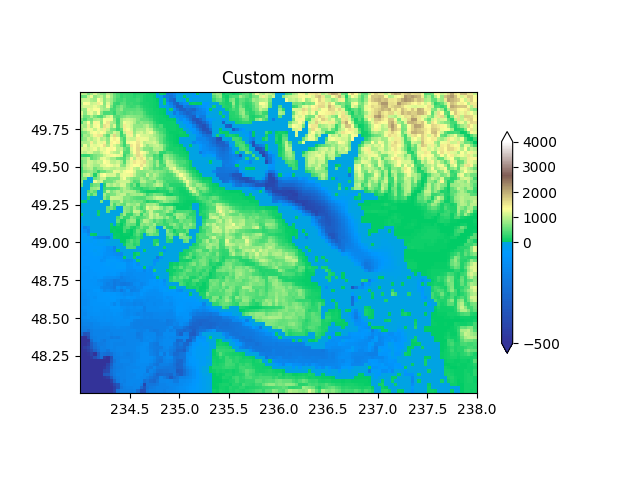
カスタム正規化: 2 つの線形範囲を手動で実装する

上記TwoSlopeNormは、独自の基準を定義するための便利な例です。カラーバーを機能させるには、ノルムの逆を定義する必要があることに注意してください。

class MidpointNormalize(colors.Normalize):
    def __init__(self, vmin=None, vmax=None, vcenter=None, clip=False):
        self.vcenter = vcenter
        super().__init__(vmin, vmax, clip)

    def __call__(self, value, clip=None):
        # I'm ignoring masked values and all kinds of edge cases to make a
        # simple example...
        # Note also that we must extrapolate beyond vmin/vmax
        x, y = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1.]
        return np.ma.masked_array(np.interp(value, x, y,
                                            left=-np.inf, right=np.inf))

    def inverse(self, value):
        y, x = [self.vmin, self.vcenter, self.vmax], [0, 0.5, 1]
        return np.interp(value, x, y, left=-np.inf, right=np.inf)


fig, ax = plt.subplots()
midnorm = MidpointNormalize(vmin=-500., vcenter=0, vmax=4000)

pcm = ax.pcolormesh(longitude, latitude, topo, rasterized=True, norm=midnorm,
                    cmap=terrain_map, shading='auto')
ax.set_aspect(1 / np.cos(np.deg2rad(49)))
ax.set_title('Custom norm')
cb = fig.colorbar(pcm, shrink=0.6, extend='both')
cb.set_ticks([-500, 0, 1000, 2000, 3000, 4000])

plt.show()